Solution:
Given that the mean weights of 26 dogs is 59 ounces, and the standard deviation is 14 ounces, this implies that
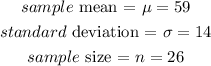
If the confidence level is 99%, this implies that the critical value is evaluated as
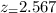
The margin of error is expressed as
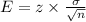
thus, the margin of error is evaluated to be

Hence, the limits of confidence interval are given by:
H