Question

A manufacture has been selling 1700 television sets a week at $390 each. A market survey indicates that for each $20 rebate offered to a buyer, the number of sets sold will increase by 200 per week.a) Find the function representing the demand p(x), where x is the number of the television sets sold per week and p(x) is the corresponding price.p(x)= ?b) How large rebate should the company offer to a buyer, in order to maximize its revenue? Please write answer in dollars. c) If the weekly cost function is 110500 + 130x, how should it set the size of the rebate to maximize its profit? Please write answer in dollars.

Answer 1

For each $20 rebate offered to a buyer, the number of sets sold will increase by 200 per week: The slope is (-20/200)

Formula of the slope:

`m=(f(x_2)-f(x_1))/(x_2-x_1)`

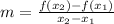
For the given situation:

`\begin{gathered} f(x_2)=p(x) \\ x_2=x \\ \\ f(x_1)=390 \\ x_1=1700 \\ \\ -(20)/(200)=(p(x)-390)/(x-1700) \end{gathered}`

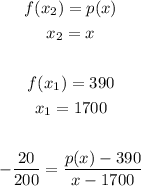
Use the equation above to solve p(x) in terms of x:

`\begin{gathered} -(1)/(10)=(p(x)-390)/(x-1700) \\ \\ (p(x)-390)/(x-1700)=-(1)/(10) \\ \\ p(x)-390=-(1)/(10)(x-1700) \\ \\ p(x)-390=-(1)/(10)x+(1700)/(10) \\ \\ p(x)-390=-(1)/(10)x+170 \\ \\ p(x)=-(1)/(10)x+170+390 \\ \\ \\ \\ p(x)=-(1)/(10)x+560 \end{gathered}`

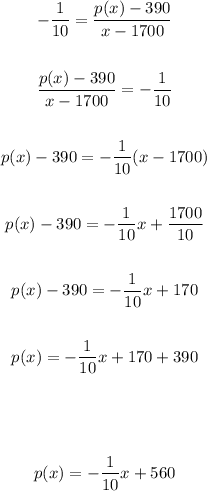
Then, the function representing the demand p(x) is:

`p(x)=-(1)/(10)x+560`

_________________

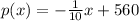
b) The largest value x can be is the value when p(x)=0: