Question

Solve the following system of equations: 3x − 2y = 6 6x − 4y = 12

Answer 1

6x - 4y = 12...divide everything by 2
3x - 2y = 6

u notice it is the same as ur other equation...this means the lines are coincident...they are the same line and therefore, have infinite solutions.

Answer 2

The system will have infinite many solution.

Explanation:

Given system of equations: 3x − 2y = 6 and 6x − 4y = 12

We have to solve for the system of equation.

Consider the given system of equations:

3x − 2y = 6 ...............(1)

6x − 4y = 12 ..............(2)

Consider equation (2) ,

6x − 4y = 12

Divide equation by 2, we get,

3x - 2y = 6

Which is same as equation (1) ,

Thus, the system will have infinite many solution.

For a system of equation having infinite solution following condition holds:

`(a_1)/(a_2)=(b_1)/(b_2)= (c_1)/(c_2)`

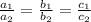
here,
`a_1=3 , b_1=-2,c_1=6\\\\a_2=6 , b_2=-4,c_2=12`

Thus, we get,

`(3)/(6)=(-2)/(-4)= (6)/(12)=(1)/(2)`

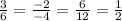
Thus, the system will have infinite many solution.