Question

How many solutions does the equation cos(6x)=1/2 have on the interval (0, 2pi)?

Answer 1

The number of possible solution of the trignometric equation are:

12

Explanation:

We have to find the solution of the trignometric equation which is given as:

`\cos(6x)=(1)/(2)`

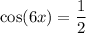
Now, the solution of the trignometric equation is the possible value of x such that the equation holds true.

Now we know that:

`\cos((\pi)/(3))=(1)/(2)`

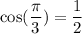
Also,

`\cos(2\pi-(\pi)/(3))=(1)/(2)\\\\i.e.\\\\\cos((5\pi)/(3))=(1)/(3)`

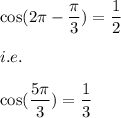
We are given that:

0<x<2π.

this means that:

0<6x<12π.

Now, we have the solution as:

`6x=(\pi)/(3)\\\\\\i.e\\\\x=(\pi)/(18)`

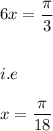
and:

`6x=(5\pi)/(3)\\\\x=(5\pi)/(18)`

`6x=2\pi+(\pi)/(3)=(7\pi)/(3)\\\\6x=4\pi-(\pi)/(3)=(11\pi)/(3)\\\\6x=4\pi+(\pi)/(3)=(13\pi)/(3)\\\\6x=6\pi-(\pi)/(3)=(17\pi)/(3)\\\\6x=6\pi+(\pi)/(3)=(19\pi)/(3)\\\\6x=8\pi-(\pi)/(3)=(23\pi)/(3)\\\\6x=8\pi+(\pi)/(3)=(25\pi)/(3)\\\\6x=10\pi-(\pi)/(3)=(29\pi)/(3)\\\\6x=10\pi+(\pi)/(3)=(31\pi)/(3)\\\\6x=12\pi-(\pi)/(3)=(35\pi)/(3)`

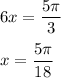
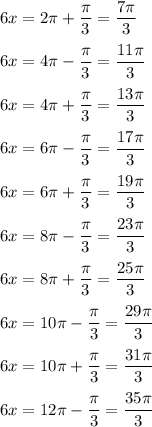
Hence, the number of possible solution of the trignometric equation are:

12

Answer 2

cos( 6 x ) = 1/2
6 x = 60° ⇒ x 1 = 10°
6 x = 300° ⇒ x 2 = 50°
6 x = 420° ⇒ x 3 = 70°
6 x = 660° ⇒ x 4 = 110°
x 5 = 130°, x 6 = 170°, x 7 = 190° , x 8 = 230°, x 9 = 250°,
x 10 = 290°, x 11 = 310°, x 12 = 350°
Answer: there are 12 solutions on the interval ( 0 , 2π ).