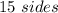Part 1) What is the sum of the interior angle measures of a 20-gon?
we know that
The formula for getting the sum of interior angle is equal to
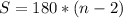
where
S is the sum of the interior angles of a regular polygon.
n is the number of sides
In this problem we have
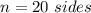
substitute in the formula
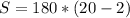
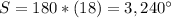
therefore
the answer Part 1) is
the sum of the interior angle measures of a 20-gon is

Part 2) What is the measure of one interior angle of a regular 12-gon?
The formula for getting the sum of interior angle is equal to
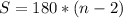
where
S is the sum of the interior angles of a regular polygon.
n is the number of sides
In this problem we have

substitute in the formula
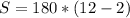
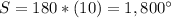
Divide the sum of the interior angles by the number of sides to obtain the measure of one interior angle
so

therefore
the answer Part 2) is
the measure of one interior angle of a regular 12-gon is
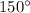
Part 3) No diagram given
Part 4) What is the measure of an exterior angle of a regular octagon?
we know that
The sum of exterior angles of a regular polygon is equal to
 degrees
degrees
so
Divide the sum of exterior angles by the number of sides to obtain the measure of one exterior angle
the regular octagon has
 sides
sides
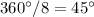
therefore
The answer Part 4) is
the measure of an exterior angle of a regular octagon is

Part 5) If the measure of an exterior angle of a regular polygon is 24, how many sides does the polygon have?
we know that
The sum of exterior angles of a regular polygon is equal to
 degrees
degrees
so
Divide the sum of exterior angles by the measure of an exterior angle to obtain the number of sides of the regular polygon
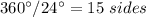
therefore
the answer part 5) is