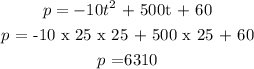Part A
To find the ticket price when the price is $16
Let us substitute the value of t = 16
p = -10 x (16 x16) + 500 x 16 + 60
p = -2560 + 8000 + 60
p =$ 5500
Part B
To get the maximum profit, we will have to differentiate P with respect to t
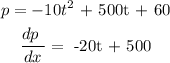
The maximum profit will be obtained when the derivative is zero
-20t + 500 = 0
20t = 500
t = 500/20
t = 25
This means that the ticket price has to be $25 so as to obtain the maximum price
Part C
The maximum profit will be obtained by substituting t = 25 into the original equation