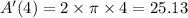Question

A) Find the average rate of change of the area of a circle with respect to its radius r as r changes from 4 to each of the following.

(i) 4 to 5 _______

(ii) 4 to 4.5 _______

(iii) 4 to 4.1 _______


(b) Find the instantaneous rate of change when r = 4.

A'(4) = ______

Answer 1

a)1. 28.26

2. 26.70

3. 25.44

b) 25.13

Explanation:

We are given the following information in the question:

Area of circle

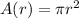`A(r) = \pi r^2`, where r is the radius of circle.

a) Formula:

Rate of change of area of circle =
`\displaystyle(A(r_2) - A(r_1))/(r_2-r_1)`

Putting the given values we get:

1. Rate of change of circle when radius changes from 4 to 5

`\displaystyle(\pi (5)^2- \pi (4)^2)/(5-4) = 9\pi = 28.26`

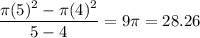
2. Rate of change of circle when radius changes from 4 to 4.5

`\displaystyle(\pi (4.5)^2- \pi (4)^2)/(4.5-4) =26.70`

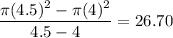
3. Rate of change of circle when radius changes from 4 to 4.1

`\displaystyle(\pi (4.1)^2- \pi (4)^2)/(4.1-4) =25.44`

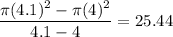
b) Instantaneous rate of change

`\displaystyle(d(A(r)))/(dr) = (d(\pi r^2))/(dr) = 2\pi r`

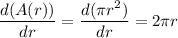
When r = 4

`A'(4) = 2* \pi * 4 = 25.13`