Question

For the feasibility region shown below, find the maximum value of the function P=2x+3y.

Answer 1

Let

A--------> the corner point in the graph
`(0,0)`

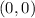
B--------> the corner point in the graph
`(0,8)`

C--------> the corner point in the graph
`(6,5)`

D--------> the corner point in the graph
`(8,0)`

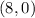
we know that

The function P is equal to

`P=2x+3y`

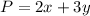
Step
`1`

Evaluate the function P in each corner point

point
`A(0,0)`

`x=0\\ y=0\\ PA=2*0+3*0\\ PA=0`

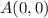
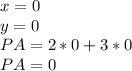
point
`B(0,8)`

`x=0\\ y=8\\ PB=2*0+3*8\\ PB=24`

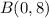
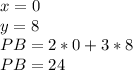
point
`C(6,5)`

`x=6\\ y=5\\ PC=2*6+3*5\\ PC=27`

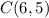
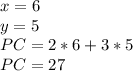
point
`D(8,0)`

`x=8\\ y=0\\ PD=2*8+3*0\\ PD=16`

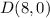
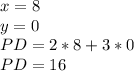
the maximum value of P is for the point C

`PC=27`

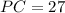
therefore

the answer is

The maximum value of the function P is
`27`

Answer 2

Corner points in this graph are: ( 0,0 ) ( 0,8 ) ( 5,6 ) and ( 8, 0 ).
If we plug those values in : P = 2 x + 3 y
P ( 0,0 )= 0
P ( 0,8 ) = 2 * 0 + 3 * 8 = 24
P ( 6 , 5 ) = 2 * 6 + 3 * 5 = 12 + 15 = 27
P ( 8 , 0 ) = 2 * 8 + 3 * 0 = 16
The maximum value is:
P max ( 6 , 5 ) = 27