Question

In the Cartesian plane xOy (the same unit of measure - cm - is used on the axes) onecharge q₁ = 4 x 10°C is placed in point (3,0), and a second charge q2 = 12 x 107C isplaced in point (0,6). What is the intensity of the resulting force acting on charge q³ = 10°C placed at the source (approximate Coulomb constant k with 9 x 10° Nm²/C²)?A) 5 NB) 5 x 10¹ NC) -1 ND) 10¹ NE) 7 N

Answer 1

A) 5 N

Step-by-step explanation

Given:

• Charge q₁ = -4 x 10⁻⁷ C

,

• The position of q₁, (3, 0)

,

• Charge q₂ = 12 x 10⁻⁷ C

,

• The position of q₂, (0, 6)

,

• Charge q₃ = 10⁻⁶ C

,

• The position of q₃, (0, 0)

Find:

• The intensity of the resulting force acting on q₃, F

Charges q₁ and q₃ have opposite charges, so q₁ exerts an attraction force on q₃. On the other hand, q₂ has the same sign as q₃, so q₂ exerts a repulsion force on q₃. So, we have,

The magnitude of the force exerted by q₁ is given by Coulomb's law,

`F_1=k\cdot(q_1q_3)/(r_1^2)`

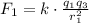
Where r₁ is the distance between charges q₁ and q₃ in meters,

`r_1=3cm=0.03m`

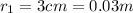
So, the force F₁ is,

`F_1=9\cdot10^9Nm^2/C^2\cdot(4\cdot10^(-7)C\cdot1\cdot10^(-6)C)/(0.03^2m^2)=4N`

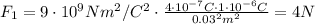
Similarly, the force exerted by q₂ on q₃ is given by,

`F_2=k\cdot(q_2q_3)/(r_2^2)`

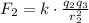
Where r₂ is the distance between q₂ and q₃ in meters,

`r_2=6cm=0.06m`

So, the force F₂ is,

`F_2=9\cdot10^9Nm^2/C^2\cdot(12\cdot10^(-7)C\cdot1\cdot10^(-6)C)/(0.06^2m^2)=3N`

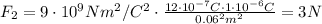
As illustrated in the diagram above, these two forces are perpendicular, so the resultant is the hypotenuse of the right triangle they form. By the Pythagorean Theorem,

`F=√(F_1^2+F_2^2)=√(4^2N^2+3^2N^2)=√(16N^2+9N^2)=√(25N^2)=5N`

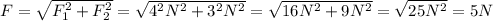
Hence, the resulting force's intensity is 5 N.