Question

Discontunuity of f(x) = x^2 plus 2x over x plus 2

Answer 1

When we have a function like:

`f(x) = (g(x))/(h(x))`

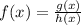
This function will have a discontinuity only if it diverges, and a divergence can happen when the denominator is equal to zero and the numerator is different than zero.

In this case, we have the equation:

`f(x) = (x^2 + 2*x)/(x + 2)`

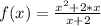
Here the denominator is:

h(x) = x + 2

This is equal to zero when:

x + 2 = 0

x = -2

Now we need to see what happens with the numerator when x = -2

g(-2) = (-2)^2 + 2*(-2) = 0

Is equal to zero.

Then we need to see the limit when x -> -2, and use the L'Hopital theorem.

`\lim_(x \to \ - 2) (x^2 + 2*x)/(x + 2)`

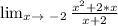
Because we have zero over zero at that point, we need to look at the quotients of the derivatives of both numerator and denominator.

`\lim_(x \to \ - 2) (2*x+ 2)/( 2) = (2*-2 + 2)/(2) = -1`

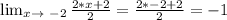
Then the function does not diverge, then the function has no discontinuity.

We also could look at the graph of f(x) to see it:

Our function is a linear function, and this is because the numerator is x times the denominator, then the function is:

f(x) = x.