Question

If you vertically compress the absolute value parent function, F(x)=|x|, by multiplying by 3/4, what is the equation of the new function?

A. G(x)= |3/4x| B. G(x)=3/4 |x|

C. G(x)=|x+3/4| D. G(x)= |x|-3/4

Answer 1

Option (b) is correct.

`f(x)=(3)/(4)|x|`

Explanation:

Given: The parent function
`f(x)=|x|`

We have to find the equation of the new function when given that the absolute parent function is vertically compress by multiplying by
`(3)/(4)`

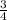
Since, given the absolute function
`f(x)=|x|`

Since, The graph is multiplied by
`(3)/(4)`

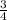
Vertically compressed or stretched

For any graph y = f(x),

A vertically compression (stretched) of a graph is compressing the graph toward x- axis.

• if k > 1 , then the graph y = k• f(x) , the graph will be vertically stretched by multiplying each y coordinate by k.

• if 0 < k < 1 if 0 < k < 1 , the graph is f (x) vertically shrunk by multiplying each of its y-coordinates by k.

• if k should be negative, the vertical stretch or shrink is followed by a reflection across the x-axis.

Here, the fraction
`(3)/(4)=0.75` so, the graph is f (x) vertically shrunk by multiplying each of its y-coordinates by k.

That is The new function when given that the absolute parent function is vertically compress by multiplying by
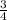`(3)/(4)` is
`f(x)=(3)/(4)|x|`

Answer 2

Option B: G(x) = 3/4 |x|, nevertheless that is the same that G(x) = |3/4x|.

Note that given that 3/4 is less than 1 the original function is compressed.