Question

The Figure Shows a curve C and a contour map of a function whose gradient is continuous. Integral in region C Nabla F dot dr

Answer 1

The value of
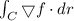`\int _C\bigtriangledown f\cdot dr` is 40.

Explanation:

It is given that the gradient of function is continuous.

By fundamental theorem for line integrals,

`\int _C\bigtriangledown f\cdot dr=f(Q)-f(P)`

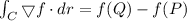
Where, C starts from P and end at the point Q.

We have to find the value of
`\int _C\bigtriangledown f\cdot dr`.

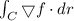The function is defined from contour line 10 to contour line 50.

`\int _C\bigtriangledown f\cdot dr=50-10`

`\int _C\bigtriangledown f\cdot dr=40`

Therefore the value of
`\int _C\bigtriangledown f\cdot dr` is 40.

Answer 2

Given figures along the curve of C are: 10, 20, 30, 40, 50

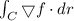∫c Nabla f * dr ⇒ f(B)−f(A)= 50 − 10 = 40