When talking about the stress and strain of a material, the behavior can be very diverse. When the exercise gives us the Modulus, it refers to Young's modulus, which is the slope where the curve strain-stress is linear. On this part of the curve, we have the following equation:
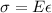
Where sigma is the tension, E is Young's modulus and epsilon is the change in length. Considering the data from our problem, we need first to calculate the area of the wire. It is:
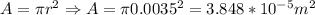
Now we have all the data we need. Considering the tension sigma is force over area, we can write the first equation as:
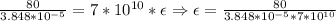
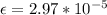
This value is adimensional. It represents how much of the original length is changed, so we still need to multiply it by the original length, which gives us:
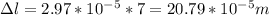
This leaves us with alternative a) 20.788e-5m