Answer: graph E.
A geometric sequence can be written as:
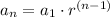
where:
a₁ = first term = 4
r = ratio = 0.5
Substituting the numbers, we have:
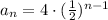
or else
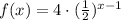
This is an exponential function with base less than 1. Therefore, we can exclude graph C (which depicts a linear function), and graphs A and D (which depict an exponential function with base greater than 1).
In order to choose between graph B and E, let's evaluate the function in two different points:
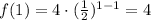
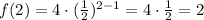
Therefore, we need to look for the graph passing through the points (1, 4) and (2, 2). That is graph E.