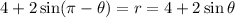Question

What type of limaçon is graphed by the polar equation = 4+2 sin theta Identify the axis of symmetry and horizontal and vertical interceptsWrite a short paragraph explaing how to do this

Answer 1

Given:

`r=4+2\sin\theta`

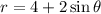
First, we take a look at the constant and the value of the term to determine the type of limacon present.

Since 4 > 2, this is an example of a dimpled limacon.

Now, to find the vertical intercepts, we need to substitute θ=π/2 and θ=3π/2:

`\begin{gathered} r=4+2\sin\theta \\ r=4+2\sin((\pi)/(2)) \\ r=6 \\ ---------- \\ r=4+2\sin((3\pi)/(2)) \\ r=2 \\ \therefore y=-2 \end{gathered}`

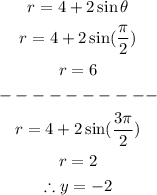
Therefore, the vertical intercepts of the equation are (0, 6) and (0, -2)

Next, to find the horizontal intercepts, we will substitute θ=0 and θ=π:

`\begin{gathered} r=4+2\sin\theta \\ r=4+2\sin0 \\ r=4 \\ -------- \\ r=4+2\sin(\pi) \\ r=4 \\ \therefore x=-4 \end{gathered}`

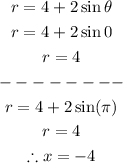
With this, we know that the horizontal intercepts are (4, 0) and (-4, 0)

The given equation is symmetric about the y-axis:

`4+2\sin(\pi-\theta)=r=4+2\sin\theta`