Question

Which of the following inequalities matches the graph? graph of an inequality with a solid line through the points (0, −2) and (2, 1)with shading above the line

3x − 2y greater than or equal to 4
 3x − 4y less than or equal to 2
 3x − 2y less than or equal to 4
 The correct inequality is not listed.

Answer 1

1) Equation of the line

Slope, m = [-2 -1]/[0 - 2] = -3 / -2 = 3/2
y-intercept, b = -2

y = 3x/2 - 2


2) Inequality
The points over the line have y-coordinate greaetr than the value of the line, then

y ≥ 3x/2 - 2

2y ≥ 3x - 4

3x - 2y ≤ 4

3) Answer: 3x - 2y less than or equal to 4.

Answer 2

The correct option is 3.

Explanation:

It is given that graph of an inequality with a solid line through the points (0, −2) and (2, 1) with shading above the line.

The equation of solid line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

`y+2=(1+2)/(2-0)(x-0)`

`y+2=(3)/(2)x`

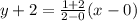
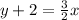
The y-intercept of the line is -2 and the shaded region is shading above the line. So, (0,0) must be lies in the shaded region.

Check the related equation by point (0,0).

`0+2=(3)/(2)(0)`

`2=0`

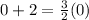
The statement is true if and only if the sign is greater than or equal instead of equal.

The required inequality is

`y+2\geq (3)/(2)x`

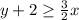
Multiply both sides by 2.

`2y+4\geq 3x`

`4\geq 3x-2y`

`3x-2y\leq 4`

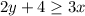
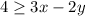
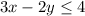
Therefore option 3 is correct.