Question

The function f(t) = t2 4t − 14 represents a parabola.

part a: rewrite the function in vertex form by completing the square. show your work. (6 points)

part b: determine the vertex and indicate whether it is a maximum or a minimum on the graph. how do you know? (2 points)

part c: determine the axis of symmetry for f(t). (2 points)

Answer 1

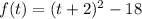`f(t)=(t+2)^2 -18` (vertex form)

Vertex(-2,-18), minimum

axis of symmetry at x= -2

Explanation:

f(t) = t^2+ 4t − 14

(a) Apply completing the square method

Take middle term +4, divide it by 2 and then square it

4/2= 2 , (2)^2 = 4

add and subtract 4

f(t) = (t^2+ 4t +4) -4− 14

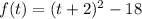`f(t)=(t+2)^2 -18` (vertex form)

(b) Vertex form is y=a(x-h)^2 + k

vertex is (h,k)

when 'a' is positive then vertex is at minimum

when 'a' is negative then vertex is maximum

`f(t)=(t+2)^2 -18`

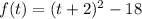
a=1, h=-2 and k= -18

vertex is (-2,-18) , a= 1 that is positive

so it is a minimum

(c) Axis of symmetry at x=h

so axis of symmetry at x= -2