Answer:
Explanations:
The central angle of a regular polygon of n sides is given as:
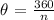
Since this is a regular hexagon, there are 6 sides
n = 6
Therefore:
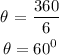
The area of a regular hexagon is given as:
![\begin{gathered} \text{Area = }\frac{3\sqrt[]{3}}{2}a^2 \\ \text{where a is the side length} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/phzjckzlwe9wtfn2xzd8.png)
The side length of the hexagon is 24 in.
That is, a = 24
Substitute a = 34 into the formula for the area above:
![\begin{gathered} \text{Area = }\frac{3\sqrt[]{3}}{2}*24^2 \\ \text{Area = }\frac{3\sqrt[]{3}}{2}*576 \\ \text{Area = }1496.49in^2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/cnjuf4ke0gjdhgxpfptj.png)
The Apothem = (2 x Area) / Perimeter
Perimeter of a regular hexagon = 6a
Perimeter = 6 x 24
Perimeter = 144 in
Apothem = (2 x 1496.49) / 144
Apothem = 20.79