Question

Given a regular hexagon with side length of 24 in, find:a. the measure of a central angleb. the apothemc. the area(round each answer to the nearest hundredth)

Answer 1

Answer:

Explanations:

The central angle of a regular polygon of n sides is given as:

`\theta\text{ = }(360)/(n)`

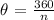
Since this is a regular hexagon, there are 6 sides

n = 6

Therefore:

`\begin{gathered} \theta\text{ = }(360)/(6) \\ \theta=60^0 \end{gathered}`

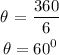
The area of a regular hexagon is given as:

`\begin{gathered} \text{Area = }\frac{3\sqrt[]{3}}{2}a^2 \\ \text{where a is the side length} \end{gathered}`

The side length of the hexagon is 24 in.

That is, a = 24

Substitute a = 34 into the formula for the area above:

`\begin{gathered} \text{Area = }\frac{3\sqrt[]{3}}{2}*24^2 \\ \text{Area = }\frac{3\sqrt[]{3}}{2}*576 \\ \text{Area = }1496.49in^2 \end{gathered}`

The Apothem = (2 x Area) / Perimeter

Perimeter of a regular hexagon = 6a

Perimeter = 6 x 24

Perimeter = 144 in

Apothem = (2 x 1496.49) / 144

Apothem = 20.79