Question

Help me plsssssssssssssssssss

Answer 1

The function that best models the given data is;

B. h(t) = -6.73·t² + 14.19·t + 0.83

Explanation:

The data in the given table is presented as follows

`\begin{array}{cccccc}Time, \, t(s)&0&0.5& 1.0 & 1.5& 2.0\\Height, \, h \, (m) & 1.0 & 5.42 & 9.71 & 5.9 & 2.6\end{array}`

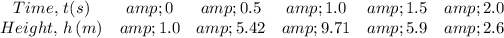
Where;

Time, t(s) is the independent variable

Height, h(m) is the dependent variable

Therefore, we have;

When t = 0, h = 1.0

From the given functions, we have the following table of the result of the function generated with Microsoft Excel

`\begin{array}{cccccc}\\t & h & A & B & C& D\\0 & 1.0 & 1.22 & 0.83& 0.83& 1.22\\0.5 & 5.42 & 5.26 & 6.2425 & 9.6075 & 10.17\\1 & 9.71 & 4.39 & 8.79 & 21.75 & 24.03 \\ 1.5 & 5.9 & -1.39& 6.9725& 37.2575 &42.8\\2& 2.6 & -12.08 & 2.29 & 56.13 & 66.48\end{array}`

By comparison, the function that nest models the given data is the function 'B', given as follows;

h(t) = -6.73·t² + 14.19·t + 0.83.