Answer:
a.Dimension of B=
![[LT^(-2)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/zm7gnycbhs9u1p9bdmjwl6y3rvp42slh7k.png)
b.Dimension of A=
![[L]](https://img.qammunity.org/2017/formulas/mathematics/high-school/ksr0915lydp6p0l3rm0vrajjvm101sp5gh.png)
Explanation:
We are given that
a.Suppose that the displacement of an object is related to time according to the expression
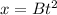
We have to find the dimension of B
Dimension of time=T
Dimension of displacement =L
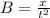
Substitute the value then we get
Dimension of B=
![(L)/(T^2)=[LT^(-2)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/1qxvbbxcacdujqzhy7idkrhn4dsk6hljiq.png)
b.A displacement is related to the time as
x=A sin(2ft)
Where A and f are constants.
We have to find the dimensions of A.
We know that trigonometric function is dimensionless.
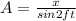
Substitute the value then we get
Dimension of A=
![[L]](https://img.qammunity.org/2017/formulas/mathematics/high-school/ksr0915lydp6p0l3rm0vrajjvm101sp5gh.png)