Answer:
The value of second quantity is 27
Explanation:
Inverse variation can be represented by the equation xy=k or
 i.e,
i.e,
y varies inversely as x , if there is some nonzero constant k such that, xy =k or
 where x≠0 and y≠0.
where x≠0 and y≠0.
Given: Two quantities vary inversely.
Let x be the first quantity and y be the second quantity if they vary inversely.
then, by definition of inverse variation;
 .....[1]
.....[1]
Substitute the value of x=15 and y=18 to solve for k;

Multiply both sides by 15 we have;

Simplify:
k=270
now, find the second quantity y using same method when x=10.
then;
after substituting the value of x=10 and k=270 in [1] ;
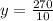
Simplify:
y= 27
Therefore, the second quantity value i.e,y = 27