Question

For the simple harmonic motion equation d=5sin((pi/4)t), what is the period?. .

Answer 1

The period of given harmonic function is 8

Explanation:

Given: The simple harmonic motion

`d=5\sin((\pi)/(4)t)`

It is equation of simple harmonic motion.

We need to find the period of this function. It is sine function.

As we know the period of sine function is 2π

Period, sin x = 2π

If coefficient x is 1 then period is 2π

Period, sin (ax) = 2π/a

If coefficient of x is "a" then period is 2π divide by a

`\sin(ax)\rightarrow \sin((\pi)/(4)t)`

`a\rightarrow (\pi)/(4)`

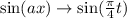
Period of given harmonic motion:

`\Rightarrow (2\pi)/(\pi/4)`

`\Rightarrow 8`

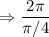
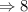
Hence, The period of given harmonic function is 8

Answer 2

8

Explanation:

The given simple harmonic motion equation is:

`d=5sin((\pi)/(4))t`

Comparing the above equation with,
`y=asinbx`, we have

a=5 and
`b=(\pi)/(4)`

Now, period of the simple harmonic motion equation is given as=
`(2\pi)/(|b|)`

=
`(2\pi)/(|(\pi)/(4)|)`

=
`8`

Thus, the period of the given simple harmonic motion equation
`d=5sin((\pi)/(4))t` is 8.