Question

Divide f(x) by d(x), and write a summary statement in the form indicated.. . f(x) = x4 + 4x3 + 6x2 + 4x + 5; d(x) = x2 + 1. . A. f(x) = (x2 + 1)( x2 + 4x + 5) + 12x - 15. B. f(x) = (x2 + 1)( x2 + 4x + 5). . C. f(x) = (x2 + 1)( x2 - 4x + 5). . D. f(x) = (x2 + 1)( x2 - 4x + 5) + 12x - 16

Answer 1

Option B is correct.

Explanation:

We given with two polynomials.

`f(x)=x^4+4x^3+6x^2+4x+5`

`d(x)=x^2+1`

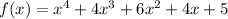
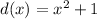
We have to check which given statement is correct.

For this divide f(x) by d(x)

Division is shown in pic.

After division we get,

Quotient = x² + 4x + 5

Remainder = 0

If, a is dividend , b is divisor , q is quotient and r is remainder ,

then by division algorthium it can be written as ,

a = bq + r

⇒ f(x) = ( x² + 1 )( x² + 4x + 5 ) + 0

f(x) = ( x² + 1 )( x² + 4x + 5 )

Therefore, Option B is correct.

Answer 2

f ( x ) : d ( x ) =
`(x^(4) + 4 x^(3) + 6 x^(2) + 4x + 5 ) : ( x^(2) + 1 ) =`
= x² + 4 x + 5
Answer:
B ) f ( x ) = ( x² + 1 ) ( x² + 4 x + 5 )