Question

A projectile is launched with a velocity of 25 m/s at an angle of 20 degrees with respect to the horizontal. What is its initial velocity along the x-axis?

Select one:
a. 10 m/s
b. 23.49 m/s
c. 18.5 m/s
d. 75 m/s
e. None of the choices give.


A projectile is launched with a velocity of 25 m/s at an angle of 20 degrees with respect to the horizontal. What is its initial velocity along the y-axis?

Select one:
a. 2.09 m.s
b. 4.21 m/s
c. 17.10 m/s
d. 8.55 m/s
e. None of the choices given.

A projectile is launched with a velocity of 25 m/s at an angle of 20 degrees with respect to the horizontal. How long will it take for it to reach the top of its flight?

Select one:
a. 5.21 s
b. 3.28 s
c. 1.74 s
d. .87 s
e. None of the choices given.
A projectile is launched with a velocity of 25 m/s at an angle of 20 degrees with respect to the horizontal. What is its range?



Select one:
a. 40.8 m
b. 81.6 m
c. 33.21 m
d. 20.4
e. None of the choices given.

Answer 1

b. 23.49 m/s

d. 8.55 m/s

d. .87 s

a. 40.8 m

Step-by-step explanation:

The initial along the x-axis is given by the following formula:

`V_(ox) = V_(o)Cos\theta\\\\V_(ox) = (25\ m/s)(Cos\ 20^(o))\\\\V_(ox) = 23.49\ m/s`

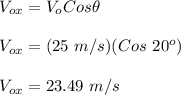
Hence, the correct option is:

b. 23.49 m/s

The initial along the x-axis is given by the following formula:

`V_(oy) = V_(o)Sin\theta\\V_(oy) = (25\ m/s)(Sin\ 20^(o))\\V_(oy) = 8.55\ m/s`

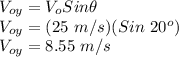
Hence, the correct option is:

d. 8.55 m/s

Now, for the time to reach maximum height:

`t = (V_(o)Sin\theta)/(g)\\\\t = ((25\ m/s)Sin\ 20^(o))/(9.8\ m/s^(2))\\\\t = 0.87\ s`

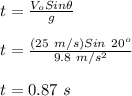
Hence, the correct option is:

d. .87 s

For the range of projectile:

`R = (V_(o)^(2)\ Sin\ 2\theta)/(g)\\\\R = ((25\ m/s)^(2)(Sin\ 40^(o)))/(9.8\ m/s^(2))\\\\R = 40.9\ m`

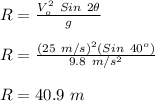
Hence, the closest option is:

a. 40.8 m