Question

A car starts from rest and accelerates uniformly at 3.0 m/s2. A second car starts from rest 6.0 seconds later at the same point and accelerates uniformly at 5.0 m/s2. How long does it take the second car to overtake the first car?

Answer 1

20.62 seconds

Explanation:

Intially, the first car starts from rest, therefore its displacement through the first 6 seconds can be found as follows:

`d=(at^(2) )/(2) =(3*6^(2) )/(2)\\d= 54 m`

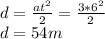
Then, we need to find out its velocity at this point, which would be the first car's initial velocity for the second moment, when the second car accelerates:

`v_(1) =at=3*6=18 m/s`

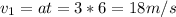
To find out the moment that the second car overtakes the first one we should equal both cars' displacement equations and solve for t, keep in mind that a 54 m head start should be added to the first car's displacement:

`v_(1)t + (a_(1)t^(2))/(2)+54 =(a_(2)t^(2))/(2)\\18t + (3t^(2))/(2)+54 =(5t^(2))/(2)\\t^(2) -18t -54 = 0`

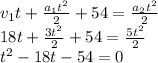
Solving for t will yield a positive and a negative answer, since time can't be negative, only the positive answer should be considered, therefore, t = 20.62 s

Answer 2

5(3)(t+6)^2 = .5(5)(t)^2
t=20.62 seconds

20.62 seconds