Question

What is the 22nd term of the arithmetic sequence where a1 = 8 and a9 = 56 ?

Answer 1

a 9 = a 1 + 8 d
56 = 8 + 8 d
8 d = 48
as d is equal to 6

so a22=a1+21d
so we get by putting value 8+126
which is 134

Answer 2

The 22nd term of the arithmetic sequence is 134.

Explanation:

Given: The arithmetic sequence where
`a_1=8` and
`a_9=56`

We have to find the 22 term of the arithmetic sequence.

Consider the given sequence with
`a_1=8` and
`a_9=56`

We know , For a given sequence in an Arithmetic sequence with first term
`a_1` and common difference d , we have,

`a_n=a_1+(n-1)d`

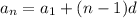
We first find the common difference "d".

`a_9=56`

`a_9=a_1+(9-1)d`

`a_1=8` , we have,

`56=8+8d`

Solve for d , we have,

48 = 8d

d = 6

Thus, 22nd term is
`a_(22)=a_1+(22-1)d`

`a_(22)=8+21\cdot 6`

`a_(22)=134`

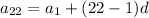
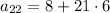
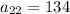
Thus, The 22nd term of the arithmetic sequence is 134.