Given function is
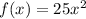
Eventually overtake means the function gets the value of f(x) at some value of x.
Consider the first option
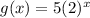
Comparing the functions
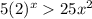
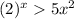
![xIn\text{ 2>2In (}\sqrt[]{5}x)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/qsgbx13aehl9nhtcy2re.png)
![\frac{x}{\text{In (}\sqrt[]{5}x)}>(2)/(In2)](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/4fziodehat6f6n7i4oas.png)
![\frac{x}{\text{In (}\sqrt[]{5}x)}>1](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/dw3sqqz1ui8sdydxb306.png)
It is true, hence g(x) eventually overtakes f(x).
Consider the function
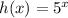
It is increasing function, it also eventually overtakes the function f(x).
Consider the function
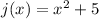
Comparing the function with f(x), we get
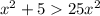
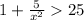
This is not true, hence j(x) is not overtaking the function f9x).
Consider the function
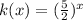
Comparing the function with f(x), we get
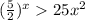
Taking log on both sides, we get
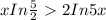
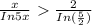
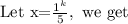

It is not true for any k value, so the function k(x) is not overtaking the function f(x).
Consider the function
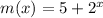
Comparing the function with f(x), we get
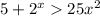
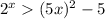
It is true for some value of x.
Hence the function m(x) overtakes the function f(x).
Consider the function
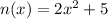
Comparing the function with f(x), we get
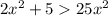
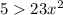
It is not true for any value of x.
Hecne the function n(x) not overtake the function f(x).
Hence the following functions are overtaken f(x).
g(x), h(x), m(x).