Answer:
AB =

Step-by-step explanation:
Here's the required formula to find distance between points :
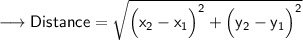
As per given question we have provided that :
Substituting all the given values in the formula to find the distance between points A(0, 1) and B(6, 3.5) :

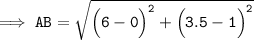
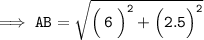
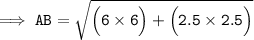
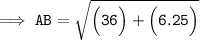


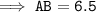
Hence, the distance between points AB is 6.5
