Question

The lateral surface area S of a right circular cone is given by (equation given below). What radius should be used to produce a cone of height 5 inches and lateral surface area 100 square inches?

a. r = 1.52138.
b. r = 4.658
c. r = 78
d. r = 6.7432

Answer 1

r = 4.658

Explanation:

Height of cone = 5 inches

Curved surface area of cone =
`\pi r * √(r^2+h^2)`

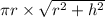
We are given that lateral surface area is 100 square inches.

So,
`100 = 3.14 * r * √(r^2+5^2)`

`100 = 3.14 * r * √(r^2+25)`

`(100)/(3.14)= r * √(r^2+25)`

`31.847= r * √(r^2+25)`

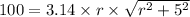
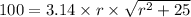
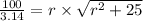
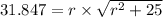
Squaring both sides

`1014.231409= r^2 * (r^2 +25)`

`1014.231409= r^4 +25r^2)`

`r^4 +25r^2-1014.231409=0`

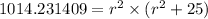
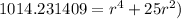
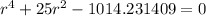
Solving this using Scientific calculator

r = 4.658

Hence the radius should be used to produce a cone of height 5 inches and lateral surface area 100 square inches is 4.658 inches

Answer 2

Given:
Lateral Area = π * r * (√h² + r²)

Lateral Area = 100 in² ; height = 5 in

I find it hard to derive the formula of r because of the radical sign. So, I'll just plug each radius to the formula to check confirm the given lateral area.

a) r = 1.52138 ⇒ LA = 24.98
b) r = 4.658 ⇒ LA = 100
c) r = 78 ⇒ LA = 19152.68
d) r = 6.7432 ⇒ LA = 177.84

The radius is B.) r = 4.658 inches