Given:
The triangle ABC and A'B'C' on a coordinate plane.
To find:
The algebraic rule that describes the dilation of ABC to A'B'C.
Solution:
From the given figure it is clear that
AB = 2 units
A'B' = 6 units
The scale factor is

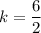
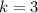
So, the scale factor is 3.
If a figure is dilated about the origin with scale factor k, then the rule of dilation is
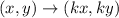
For the given problem the scale factor is 3. So, putting k=3, we get
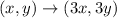
Therefore, the correct option is A.