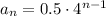Question

A geometric sequence is defined recursively by an = 4an-1. The 1st term of the sequence is 0.5. Which of the following is the explicit formula for the nth term of the sequence?

Answer 1

`\left\{\begin{array}{ccc}a_1=0.5\\a_n=4a_(n-1)\end{array}\right\\\\a_1=0.5\\a_2=0.5\cdot4=2\\a_3=2\cdot4=8\\a_4=8\cdot4=32\\a_5=32\cdot4=128\\\\a_n=a_1r^(n-1)\\\\r=a_2:a_1\to r=2:0.5=4\\\\\boxed{a_n=0.5\cdot4^(n-1)}`

Answer 2

`a_n = 0.5 \cdot 4^(n-1)`

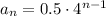
Explanation:

The explicit formula for the nth term of the geometric sequence is given by:

`a_n = a_1 \cdot r^(n-1)` ....[1]

As per the statement:

A geometric sequence is defined recursively by:

`a_n = 4 \cdot a_(n-1)` ....[2]

The 1st term of the sequence is 0.5

⇒
`a_1 = 0.5`

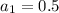
We know that:

the recursive formula for geometric sequence is given by:

`a_n = r \cdot a_(n-1)` where, r is the common ratio

Compare with [2] we have;

r = 4

Substitute the values of r = 4 and
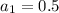`a_1 = 0.5` in [1] we have;

`a_n = 0.5 \cdot 4^(n-1)`

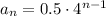
Therefore, the explicit formula for the nth term of the sequence is,
`a_n = 0.5 \cdot 4^(n-1)`