Question

which statement best describes the graph of x3 − 3x2 − 4x 12? it starts down on the left and goes up on the right and intersects the x-axis at x = −2, 2, and 3. it starts down on the left and goes up on the right and intersects the x-axis at x = −2, 4, and 3. it starts up on the left and goes down on the right and intersects the x-axis at x = −2, 2, and 3. it starts up on the left and goes down on the right and intersects the x-axis at x = −2, 4, and 3.

Answer 1

option A is correct.

Explanation:

We are given the graph of
`x^(3)-3x^(2)-4x+12`.

clearly the roots of this equation is:

`x^3-3x^2-4x+12=0\\x^2(x-3)-4(x-3)=0\\(x^2-4)(x-3)=0\\(x-2)(x+2)(x-3)=0`

⇒
`x=2`,
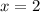`x=-2`and
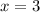`x=3` are the roots of the equation.

Hence the graph will intersect x-axis at these 3 points x=3,2 and -2.

From the graph we could clearly see that the graph starts down on the left and goes up on the right and intersects the x-axis at x=2,-2 and 3.

Hence, option A is correct.

Answer 2

it starts down on the left and goes up on the right and intersects the x-axis at x = −2, 2, and 3

Because the roots are -2, 2 and 3 and the function is negative when x is a less than - 2.