Given:
The equation of line p is
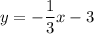
Line p and q are parallel.
To find:
The equation of line q.
Solution:
The slope intercept form of a line is

Where, m is slope and b is y-intercept.
The equation of line p is
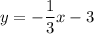
The slope of the line is
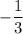 .
.
We know that the slopes of parallel lines are equal.
Line p and q are parallel. So,
Slope of line q =
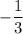
Line q passes through (6,-4) with slope
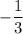 , so the equation of the line is
, so the equation of the line is
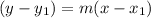
Where, m is the slope.
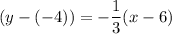
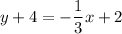
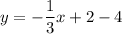
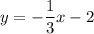
Therefore, the equation of line q is
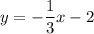 .
.