Question

Graph the first six terms of a sequence where a1 = 3 and d = -10.

Answer 1

To determine the first six terms of the arithmetic progression, add the common difference to the prior term

a1 = 3
a2 = 3 + -10 = -7
a3 = -7 + -10 = -17
a4 = -17 + - 10 = -27
a5 = -27 + -10 = -37
a6 = - 37 + -10 = -47
Plot these values in the number line.

Answer 2

3, -7, -17, -27, -37, -47

Explanation:

Given: First term: a= 3 and Common Difference, d = -10

We need to find the first six term of the sequence.

Formula:
`a_n=a+(n-1)d`

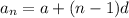
where,

`a_n` nth term of series

a is first term

n is number of term

d is common difference

For Second term, n=2

`a_2=3+(2-1)(-10) = 3-10=-7`

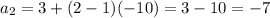
For Third term, n=3

`a_3=3+(3-1)(-10) = 3-20=-17`

For Fourth term, n=4

`a_4=3+(4-1)(-10) = 3-30=-27`

For Fifth term, n=5

`a_5=3+(5-1)(-10) = 3-40=-37`

For Sixth term, n=6

`a_6=3+(6-1)(-10) = 3-50=-47`

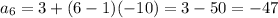
Hence, The sequence is 3, -7, -17, -27, -37, -47