Question

What are the real and complex solutions of the polynomial equation? x^4-41x^2=-400

Answer 1

`x_(1)=5;x_(2)=-5;x_(3)=4;x_(4)=-4`

Explanation:

The given expression is

`x^(4)-41x^(2) =-400`

First, we have to move all terms to the left side of the equation

`x^(4)-41x^(2)+400 =0`

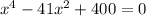
Now, we can do a change of variable to transform this relation into a quadratic one. So

`y^(2)=x^(4); y=x^(2)`

Then,
`y^(2)-41y+400=0`

Now, we applied the quadratic formula

`y_(1,2)=\frac{-b\±\sqrt{b^(2)-4ac} }{2a}`

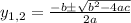
Where

`a=1;b=-41;c=400`

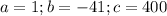
Replacing these values, we have

`y_(1,2)=\frac{-(-41)\±\sqrt{(-41)^(2)-4(1)(400)} }{2(1)}\\y_(1,2)=(41\±√((1681-1600) )/(2)=(41\±√(81) )/(2)\\ y_(1,2)=(41\±9)/(2)\\ y_(1)=(41+9)/(2)=25\\y_(2)=(41-9)/(2)=16`

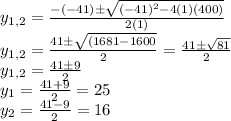
However, we need to revert the variable change

`x_(1) ^(2) =25\\\\x_(2) ^(2)=16\\x_(1)=\±5\\x_(2)=\±4`

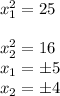
This means that the expression only have real solution, which are

`x_(1)=5;x_(2)=-5;x_(3)=4;x_(4)=-4`

Answer 2

we are given the polynomial equation x^4 - 41x^2 + + 1400 and is asked to determine the roots of the equation whether real or complex. The standard form should be the equal to the equation where -400 is up in the left side. The answers are 4 integers: 2 are negative