Question

Over 2 years, how much more does $2000 in a savings account with an apr of 4.6 compounded semiannually earn in interest than the same amount in a savings account with an apr of 4.4% compounded quarterly? A. $3.76 B. $1.88 C. $7.52 D. $15.04

Answer 1

the right answer is C. 7.52

Answer 2

C. $7.52

Step-by-step explanation

To solve this, we are going to use the compounded interest formula:

`A=P(1+ (r)/(n) )^(nt)`

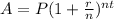
where

`A` is the final amount after
`t` years

`P` is the initial investment

`r` is the interest rate in decimal form

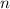`n` is the number of times the interest is compounded per year

`t` is the time in years

We know that the initial investment is $2000 and the time is 2 years, so
`P=2000` and
`t=2`. Now, for the the first account
`n=2` and
`r=(4.6)/(100) =0.046`; for the second account
`n=4` and
`r=(4.4)/(100) =0.044`. Let's calculate
`A` for both accounts:

For the first account

`A=2000(1+(0.046)/(2) )^((2)(2))`

`A=2000(1+(0.046)/(2) )^(4)`

`A=2190.45`

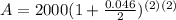
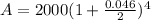
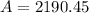
For the second account

`A=2000(1+(0.044)/(4) )^((4)(2))`

`A=2000(1+(0.044)/(4) )^(8)`

`A=2182.93`

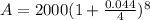
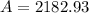
Now we just need to subtract the total amount of the second account from the total amount of the first account:

$2190.45 - $2182.93 = $7.52

The account of 4.6 compounded semiannually earn $7.52 more than the account of 4.4% compounded quarterly.