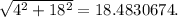Question

In the figure below the y-axis points north, the x-axis points east, and the xy-plane corresponds to the surface of the water. Suppose a boat is at point B, a submarine is 5 units below point S, and a helicopter is 13 units above point H.

Answer 1

The distance from the submarine to the boat is approximately 9.22 units, from the helicopter to the boat is 13 units, and from the submarine to the helicopter is around 18.48 units.

1. Displacement vector and distance from the submarine to the boat:

The displacement vector from the submarine to the boat is the difference between the position vectors of the two points. The position vector of the submarine is (-1, 4-5) = (-1, -1) and the position vector of the boat is (3, 4). Therefore, the displacement vector is:

(3, 4) - (-1, -1) = (3+1, 4+1) = (4, 5)

The distance from the submarine to the boat is the magnitude of the displacement vector, which is
`√(4^2 + 5^2) = {9.2195444}.`

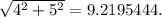
2. Displacement vector and distance from the helicopter to the boat:

The displacement vector from the helicopter to the boat is the difference between the position vectors of the two points. The position vector of the helicopter is (3, 4+13) = (3, 17) and the position vector of the boat is (3, 4). Therefore, the displacement vector is:

(3, 17) - (3, 4) = (3-3, 17-4) = (0, 13)

The distance from the helicopter to the boat is the magnitude of the displacement vector, which is
`√(0^2 + 13^2) = {13}.`

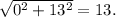
3. Displacement vector and distance from the submarine to the helicopter:

The displacement vector from the submarine to the helicopter is the difference between the position vectors of the two points. The position vector of the submarine is (-1, 4-5) = (-1, -1) and the position vector of the helicopter is (3, 4+13) = (3, 17). Therefore, the displacement vector is:

(3, 17) - (-1, -1) = (3+1, 17+1) = (4, 18)

The distance from the submarine to the helicopter is the magnitude of the displacement vector, which is
`√(4^2 + 18^2) = {18.4830674}.`

Answer 2

So the question ask to find the displacement vector and the distance from the submarine to the boat. Base on my calculation the displacement value of the given data you give is <(5-3),(1-4)(-5-0)>. I hope you are satisfied with my answer and feel free to ask for more