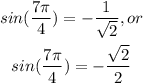Given:

To Determine: The value of the given on a unit circle
Solution
For sin 7pi/4, the angle 7pi/4 lies between 3pi/2 and 2pi (Fourth Quadrant)
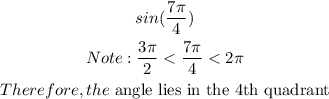
This is as shown below
In a simplified form, we have it as shown in the image below
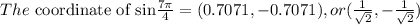
Note that sine is negative in the fourth quadrant
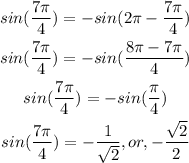
Hence,