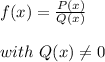Question

Do rational expressions contain logarithmic functions? A. always B. sometimes C. never

Answer 1

By definition, rational expression is the ratio of two polynomial function Q(x) and P(x), where P(x) should not be zero. Polynomial function is defined as continuous for all real number. But, Logarithmic function is continuous only for any value of x>0. Hence,Rational expression SOMETIMES contain logarithmic functions and it should not be located at the denominator.

Answer 2

The right answer is C. never

The quotient of two algebraic expressions is a fractional expression. Moreover, the quotient of two polynomials such as:

`(1)/(x) \\ \\ (3x-2)/(1+x) \\ \\ (x^2-4)/(x^2+2)`

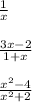
is called a rational expression. So according to this definition rational expressions does not contain logarithmic functions. In fact, a rational expression is an expression that is the ratio of two polynomials like this:

`f(x)=(P(x))/(Q(x)) \\ \\ with \ Q(x) \\eq 0`