Question

What are the coordinates of the turning point for the function f(x) = (x - 1)3 - 3? A. (-1, -3)

B. (-1, 3)

C. (1, -3)

D. (1, 3)

Answer 1

Answer: C. (1, -3)

Explanation:

Given function,

`f(x) = (x - 1)^3 - 3` -------(1)

By differentiating the above equation with respect to x,

`f'(x) = 3(x - 1)^2 - 0`

`f'(x) = 3(x - 1)^2`

At the turning point of the function f(x),

f'(x) = 0

⇒
`3(x - 1)^2 = 0`

⇒
`(x - 1)^2 = 0`

⇒
`x - 1 = 0`

⇒
`x = 1`

By substituting this value in equation (1),

We get,

f(x) = - 3

Hence, the turning point of the function f(x) is (1,-3).

⇒ Option C is correct.

Answer 2

ANSWER

The turning point is


`(1,-3).`


EXPLANATION


The function given to us is


`f(x) = (x - 1) ^(3) - 3`

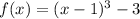
At turning point,

`f '(x) = 0`

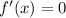
So we need to differentiate the given function and equate it to zero.



We using the chain rule of differentiation, we obtain,

`f '(x) =3 (x - 1) ^(2)`

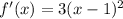
We equate this to zero to obtain,





`3 (x - 1) ^(2) = 0`



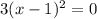
We divide through by 3.



`(x - 1) ^(2) = 0`

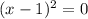
We solve for x to get,


`x - 1 = 0`



`x = 1`


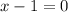
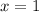
We substitute this x-value in to the function to obtain the corresponding y-value of the turning point.






`f(1) = (1- 1) ^(3) - 3`





`f(1) = 0 - 3`



`f(1) = - 3`

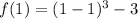
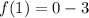
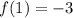
Therefore the turning point is



`(1,-3)`

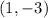
C is the correct answer.