Question

As shown in the figure above, a 50 kg box is dragged across the floor with a pulling force (Fp) of 200 N which acts at an angle of 30 degrees above the horizontal. The coefficient of kinetic friction is 0.25. What is the acceleration of the box? (Use g = 9.8 m/s2. Hint: the normal force is not equal to the weight)

Answer 1

The acceleration of the box is 2.05 m/s²

Step-by-step explanation:

The given parameters of the motion of the box are;

The mass of the box, m = 50 kg

The pulling force,
`F_p` acting on the box = 200 N

The angle at which the force acts, θ = 30° above the horizontal

The coefficient of kinetic friction,
`\mu_k` = 0.25

The normal reaction from the box resting on a flat surface, N = The weight of the box, W - The vertical component of the pulling force,
`F_(py)`

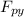
N = W -
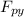`F_(py)` = m·g -
`F_p` × sin(θ)

Where;

g = The acceleration due to gravity = 9.8 m/s²

∴ N = W -
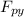`F_(py)` = m·g -
`F_p` × sin(θ) = 50 kg × 9.8 m/s² - 200 N × sin(30°)

∴ N = 490 N - 200 N × 0.5 = 390 N

The normal reaction, N = 390 N

The force of friction,
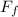`F_f` = The coefficient of kinetic friction,
`\mu_k` × The normal reaction, N

∴
`F_f` =
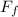`\mu_k` × N = 0.25 × 390 N = 97.5 N

The net force,
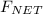`F_(NET)`, acting on the block = The pulling force,
`F_p` - The friction force,
`F_f`

∴
`F_(NET)` =
`F_p` -
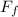
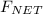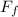`F_f` = 200 N - 97.5 N = 102.5 N

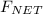`F_(NET)` = 102.5 N

According to Newton's second law of motion on the net force acting on an object, we have;

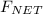`F_(NET)` = m × a

Where;

a = The acceleration of the box

∴ a =
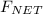`F_(NET)`/m = 102.5 N/(50 kg) = 2.05 m/s²

The acceleration of the box = a = 2.05 m/s².