Question

Find the value of x.

Answer 1

`\boxed {\boxed {\sf x=5}}`

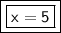
Explanation:

We are given a quadrilateral. It will be difficult to find x using this shape, but we can drop a perpendicular line and create a right triangle (refer to the attached image).

Match up the other sides. The height is equal to 4.

At the base, the longer portion is 7 because the line segment above the base is 7. Since the entire base is 10, the smaller portion must be 3 because 10-7=3.

Now we have 2 sides of a right triangle and one unknown. We can use the Pythagorean Theorem.

`a^2+b^2=c^2`

Where a and b are the legs and c is the hypotenuse.

In this triangle, 4 and 3 are the legs because they make the right angle. x is the hypotenuse because it is opposite the right angle.

• a= 4, b=3, c=x

Substitute the values into the formula.

`(4)^2+(3)^2=x^2`

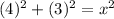
Solve the exponents.

• (4)²= 4*4= 16

`16+(3)^2=x^2`

• (3)²= 3*3= 9

`16+9=x^2 \\`

`25=x^2`

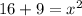
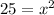
Take the square root of both sides of the equation to isolate the variable.

`√(25) =√(x^2)`

`5=x`

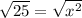
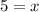
x is equal to 5.