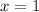Question

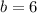Part C Find the values for a and b. Explain or show your reasoning. Answer Part D What is the y-coordinate when x = 0? Explain or show your reasoning. Answer

Answer 1

(a)

`b = 6` and
`a = 5`

(b)
`x = 1`

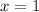
Explanation:

Given

`(x_1,y_1) = (2,2)`

`(x_2,y_2) = (4,b)`

`(x_3,y_3) = (a,8)`

`(x_4,y_4) = (6,10)`

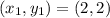
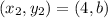
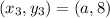
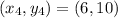
See attachment

Solving (a): The values of a and b

First, calculate the slope of the line:

`m = (y_c - y_d)/(x_c - x_d)`

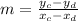
Let c = 4 and d = 1

`m = (y_4 - y_1)/(x_4 - x_1)`

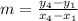
So, we have:

`m = (10 - 2)/(6 - 2)`

`m = (8)/(4)`

`m = 2`

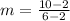
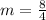
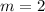
To solve for the value of b, we apply slope formula

`(y_c - y_d)/(x_c - x_d) = m`

Let c = 2 and d = 1

So, we have:

`(y_2 - y_1)/(x_2 - x_1) = m`

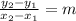
Substitute 2 for m and
`(x_1,y_1) = (2,2)` ;
`(x_2,y_2) = (4,b)`

`(b - 2)/(2) = 2`

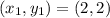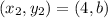
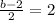
Multiply both sides by 2

`2 * (b - 2)/(2) = 2 * 2`

`b - 2 = 4`

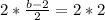
Add 2 to both sides

`b - 2 +2= 4 + 2`

`b = 6`

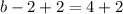
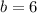
To solve for the value of a, we apply slope formula

`(y_c - y_d)/(x_c - x_d) = m`

Let c = 3 and d = 1

`(y_3 - y_1)/(x_3 - x_1) = m`

Substitute 2 for m and
`(x_1,y_1) = (2,2)` ;
`(x_3,y_3) = (a,8)`

`(8 - 2)/(a- 2) = 2`

`(6)/(a- 2) = 2`

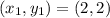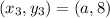
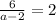
Cross Multiply

`2(a-2) = 6`

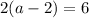
Open bracket

`2a-4 = 6`

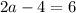
Add 4 to both sides

`2a-4+4 = 6+4`

`2a= 10`

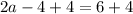
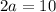
Divide both sides by 2

`a = 5`

Solving (b): The value of y when x = 0.

This point is represented as:
`(x_5,y_5) = (x,0)`

Apply slope formula

`(y_5 - y_1)/(x_5 - x_1) = m`

Substitute 2 for m and
`(x_1,y_1) = (2,2)`
`(x_5,y_5) = (x,0)`

`(0 - 2)/(x - 2) = 2`

`(- 2)/(x - 2) = 2`

`-(2)/(x - 2) = 2`

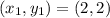
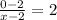
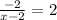
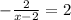
Cross Multiply

`-2 = 2 * (x - 2)`

`-2 = 2 x - 4`

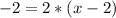
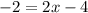
Collect Like Terms

`4 - 2 = 2x`

`2 = 2x`

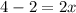
Divide both sides by 2

`1 = x`

`x = 1`