Answer:
Option 2nd is correct.
![f[g(6)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/ibqjatnxshhcdhbu8hempdjmcc6a91zsfo.png) =0.
=0.
Explanation:
Given the function:


Solve:
![f[g(6)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/ibqjatnxshhcdhbu8hempdjmcc6a91zsfo.png)
First calculate:
f[g(x)]
Substitute the function g(x)
![f[x-8]](https://img.qammunity.org/2017/formulas/mathematics/high-school/3lt3bz50eej4bgyccn4600hesl1fpyr4tw.png)
Replace x with x-8 in the function f(x) we get;

The distributive property says that:
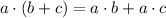
Using distributive property:

⇒
![f[g(x)] = 6x-36](https://img.qammunity.org/2017/formulas/mathematics/high-school/46u97x38hqbkh590d75lx1z3adzl2ow85e.png)
Put x = 6 we get;
![f[g(6)] = 6(6)-36 = 36-36 =0](https://img.qammunity.org/2017/formulas/mathematics/high-school/4j5fnkiubfrdrix55urtkhcdxv2g5qbi0d.png)
Therefore, the value of
![f[g(6)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/ibqjatnxshhcdhbu8hempdjmcc6a91zsfo.png) is 0.
is 0.