Question

Examine the system of equations. Which is an equivalent form of the first equation that when added to the second equation eliminates the y terms?

-5/8x + 3/4y = 12
8x + 12y = 11

A. 10x - 12y = -192
B. - 10x + 12y = 192
C. 5x - 12y = 96
D. - 5x + 12y = 96

Answer 1

if u multiply the first equation by -16, u get : 10x - 12y = - 192

and when added to the other equation, it will eliminate the y terms.

Answer 2

Option B -
`-10x+12y=192`

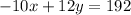
Explanation:

Given : The system of equations

`-(5)/(8)x+(3)/(4)y=12`

`8x+12y=11`

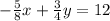
To find : Which is an equivalent form of the first equation that when added to the second equation eliminates the y terms?

Solution :

To get an equivalent equation we solve the equation by taking least common denominator,

`-(5)/(8)x+(3)/(4)y=12`

`(-5x+6y)/(8)=12`

`-5x+6y=12* 8`

`-5x+6y=96`

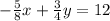
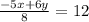
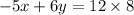
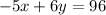
Multiply equation by 2,

`-10x+12y=192`

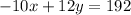
Therefore, option B is correct.