Question

Select all of the roots of x3 2x2 – 16x– 32. –1 –2 –4 1 4 5

Answer 1

In order to find the roots of the cubic equations by graphing you have to follow those steps

we have

`x^3+2x^2-16x-32`

we know that

The roots of the function are the values of x when the value of the function is equal to zero

Using a graphing tool

see the attached figure

The roots are

`x=-4\ x=-2\ x=4`

therefore

the answer is

`x=-4\ x=-2\ x=4`

Answer 2

The roots are -2,-4 and 4

B, C and E are correct.

Explanation:

Given:
`x^3+2x^2-16x-32`

We are given a cubic polynomial. We have to find the roots of the polynomial. Roots are the x-intercept of polynomial.

First we will set the polynomial to 0 and solve for x

`x^3+2x^2-16x-32=0`

`x^2(x+2)-16(x+2)=0`

`(x+2)(x^2-16)=0`

`(x+2)(x+4)(x-4)=0`
`\because a^2-b^2=(a+b)(a-b)`

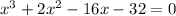
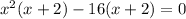
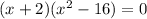
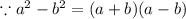
Now, we will set each factor to zero and solve for x

`x+2=0\ \ \ \ x+4=0\ \ \ \ \ \ \ x-4=0`

`x=-2,-4,4`

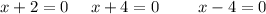
Hence, The roots are -2,-4 and 4