Question

Seth has two similar ice-cream cones, Cone A and Cone B. The slant height of Cone A is 16 inches, and the slant height of Cone B is 4 inches. What is the ratio of the volume of Cone A to the volume of Cone B?

64 : 1

8 : 1

4 : 1

16 : 1

Answer 1

64:1

Explanation:

For similar lengths, we use the relationship
`A=kB` where A and B are the measurements of the two figures' lengths and k is the scale factor.

For similar volumes, we use the relationship
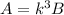`A=k^3B` where A and B are the measurements of the two figures' volumes and k is the scale factor.

Since lengths are given, we use the first formula to find k:

`16=k(4)\\k=(16)/(4)=4`

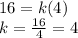
The 2nd formula also tells us that volumes are
`k^3` of each other. So

`k^3=(4)^3=64`

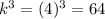
That means the larger cone has a volume that is 64 times the smaller. So the ratio is 64:1

Answer 2

The ratio of the volume of Cone A to the volume of Cone is 64 : 1. The correct answer between all the choices given is the first choice. I am hoping that this answer has satisfied your query and it will be able to help you in your endeavor, and if you would like, feel free to ask another question.