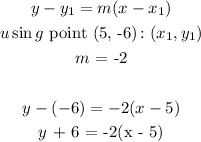Question

Determine the equation of a line in point slope form that passes through (5, -6) and (-1, 6)y- ? = ? (X - ?)

Answer 1

y + 6 = -2(x - 5)

1st unknown: -6

2nd unknown: -2

3rd unknown: 5

Step-by-step explanation:

The given points: (5, -6) and (-1, 6)

To get the equation in point slope form, we will apply the formula:

`\begin{gathered} y-y_1=m(x-x_1) \\ \\ \text{where m = slope} \\ (x_1,y_1)\text{ is a point on the line} \end{gathered}`

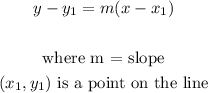
First let's find the slope of the line using the given points:

`\begin{gathered} x_1=5,y_1=-6,x_2=-1,y_2\text{ = 6} \\ \text{slope = }\frac{6\text{ - (-6)}}{-1-5} \\ \text{slope = }(6+6)/(-1-5)\text{ = }(12)/(-6) \\ \text{slope = -2} \end{gathered}`

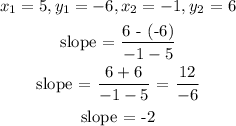
Next we pick any of the points and the slope to get point slope form:

`\begin{gathered} y-y_1=m(x-x_1) \\ u\sin g\text{ point (5, -6)}\colon(x_1,y_1) \\ m\text{ = -2} \\ \\ y-(-6)=-2\mleft(x-5\mright) \\ y\text{ + 6 = -2(x - 5)} \end{gathered}`