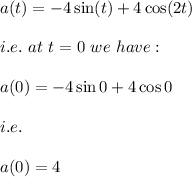A particle moves along the x-axis so that at any time t, measured in seconds, its position is given by s(t) = 4sin(t) - cos(2t), measured in feet. What is the acceleration of th…

Question

asked Dec 26, 2017 201k views

1 Answer

Rafalmag · Answer 1 · 2018-01-02T09:42:40+0000

The acceleration of the particle at time t = 0 seconds is:

4 feet per square second.

i.e. 4 ft/s²

We are given a position function in terms of the time t as:

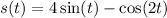
$s(t)=4\sin (t)-\cos (2t)$

Now, we are asked to find the acceeleration of the particle at time t = 0 seconds.

We know that the acceleration of a particle is given by:

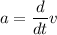
a=(d)/(dt)v

where v is the velocity of the particle which is calculated by:

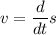
v=(d)/(dt)s

Hence, we get:

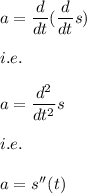
$a=(d)/(dt)((d)/(dt)s)\\\\i.e.\\\\a=(d^2)/(dt^2)s\\\\i.e.\\\\a=s''(t)$

i.e. the acceleration of the particle is the double derivative of the position.

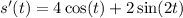
$s'(t)=4\cos (t)+2\sin (2t)$

and

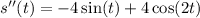
$s''(t)=-4\sin (t)+4\cos (2t)$

i.e.

$a(t)=-4\sin (t)+4\cos (2t)\\\\i.e.\ at\ t=0\ we\ have:\\\\a(0)=-4\sin 0+4\cos 0\\\\i.e.\\\\a(0)=4$